Pouvez-vous imaginer résoudre l’un des plus grands problèmes mathématiques existants, un casse-tête depuis des décennies, et rester pratiquement anonyme ? Pas de gloire, d’argent, de célébrité, d’interviews, de prix, de discours… simplement apporter sa contribution et disparaître. Cette histoire n’est pas une fiction. Son protagoniste est Grigori Perelman, un mathématicien russe.En 2003, Grigori a démontré la conjecture de Poincaré, un problème considéré pendant près d’un siècle comme l’un des plus difficiles au monde.Bien qu’il ait choisi de ne pas l’être, sa solution a fait de lui une légende.
## Les sept problèmes du millénaire
Cette histoire commence trois ans avant l’exploit de Grigori.Au début du siècle, en 2000, le Clay Mathematics Institute, une fondation scientifique aux États-Unis, a lancé un défi inédit : résoudre sept des problèmes mathématiques les plus complexes et les plus anciens qui, à l’époque, restaient sans réponse. Une récompense était promise : un prix d’un million de dollars pour chacun d’eux.
Ils ont été nommés les problèmes du millénaire. En réalité, résoudre l’un d’eux signifiait bien plus que gagner de l’argent.C’était une forme d’immortalité académique, une ascension vers un objectif que tous les mathématiciens du monde poursuivaient depuis plus d’un siècle. Ces problèmes touchaient des domaines primordiaux comme la cryptographie, la physique théorique, l’informatique ou la géométrie spatiale.
La conjecture de Poincaré se distinguait des autres. Elle semblait simple, mais sa arduousé était profonde. Formulée en 1904 par le mathématicien français Henri poincaré, elle portait sur des sphères. Sa solution ouvrait une porte vers la compréhension de l’univers.
## La conjecture de poincaré
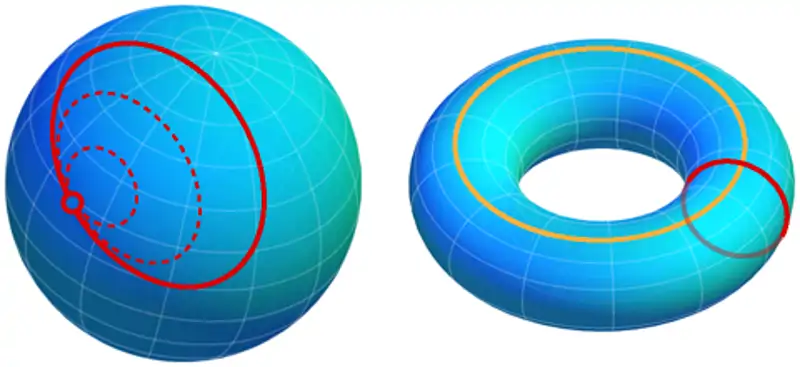
Pour l’expliquer sans formules, imaginons des objets de forme sphérique, comme une orange ou une balle. Ces objets n’ont pas de trous. Si vous dessinez un cercle sur leur surface, vous pouvez le rétrécir jusqu’à le transformer en un point, sans avoir à ouvrir les lignes. En langage mathématique,ces objets sont « simplement connexes ».
Si vous imaginez un donut, vous constaterez qu’il présente un trou. Vous ne pouvez pas rétrécir un cercle autour de ce trou sans briser ses lignes ou sans traverser la figure. La conjecture de Poincaré posait la question suivante :
« Toute forme tridimensionnelle qui n’a pas de trous et est simplement connexe est, en essence, une sphère tridimensionnelle. »
En d’autres termes, Poincaré affirmait que tout objet remplissant la première condition (le cercle qui peut être rétréci) est toujours une sphère. Cela peut sembler évident,mais le démontrer avec une précision mathématique exige une grande connaissance de l’espace et de la façon dont les formes peuvent être pliées et étirées dans des dimensions invisibles. La démonstration mathématique était si difficile que, pendant près de 100 ans, personne n’y est parvenu.
La difficulté réside dans la nécessité de donner un sens à la forme de l’univers à son niveau le plus fondamental. La solution de la conjecture devait s’appliquer à tout, à une simple orange comme au cosmos lui-même. Comment savoir si l’espace qui nous entoure n’a pas de trou invisible ? Comment définir la forme de l’ensemble quand on ne peut pas la voir de l’extérieur ?

## Le génie qui l’a résolue… et a disparu
En 2003, Grigori Perelman, né en 1966 à Léningrad, a finalement résolu l’énigme de Poincaré. Prodige dès son jeune âge, Grigori a remporté l’Olympiade internationale de mathématiques en représentant l’URSS. il s’est ensuite formé dans des centres mathématiques d’élite. il n’a jamais manifesté beaucoup d’intérêt pour la célébrité. Il était introverti, austère et aimait la pureté naturelle.
Dans les années 1990, il a commencé à travailler silencieusement sur la géométrie des formes complexes. En 2002 et 2003,il a publié une série de trois articles dans un dépôt numérique,sans passer par des revues ou des congrès. Le plus incroyable ? Ces publications contenaient une démonstration de la conjecture de Poincaré, basée sur une technique sophistiquée connue sous le nom de flux de Ricci, un outil mathématique qui « lissait » les formes complexes jusqu’à révéler leur essence.
Les mathématiciens du monde entier étaient stupéfaits. Pendant plusieurs années, diverses équipes ont examiné sa démonstration. En 2006, la grande nouvelle a été confirmée : Grigori Perelman avait résolu la conjecture de Poincaré.Le monde académique a voulu l’honorer. Il a reçu la médaille Fields, l’équivalent du prix Nobel de mathématiques, mais l’a refusée. En 2010,le Clay Institute a voulu lui remettre le million de dollars promis,mais il l’a également refusé.
## Un homme hors du système
Selon Grigori lui-même :
« Je ne veux pas être exposé comme un animal dans un zoo. Je ne veux pas recevoir de prix si la communauté mathématique n’est pas juste. Je n’ai besoin de rien. »
Depuis, Perelman vit en reclus. Il réside toujours à Saint-Pétersbourg, mais ne donne pas d’interviews, ne publie pas et n’enseigne pas dans les universités.Il a refusé des postes dans des institutions prestigieuses comme Princeton ou Stanford. C’est un homme avec un goût pur pour la connaissance, sans filtres, sans applaudissements et sans contrats.
Sur les sept problèmes du millénaire, un seul a été résolu jusqu’à présent : la conjecture de Poincaré. La solution n’est pas venue d’une institution ou d’une équipe, mais d’un homme doté d’une grande capacité mathématique et d’une éthique de béton. Qui seront les prochains génies à résoudre ce qui semble encore, à ce jour, insoluble ?
Grigori Perelman : L’Homme qui a Résolu la Conjecture de Poincaré et Disparu
Table of Contents
La Conjecture de poincaré et les Problèmes du Millénaire
En 2000, le Clay Mathematics Institute a lancé un défi de taille : résoudre sept des problèmes mathématiques les plus complexes et anciens, avec une récompense d’un million de dollars pour chacun. Ces problèmes, appelés les problèmes du millénaire, touchaient des domaines cruciaux comme la cryptographie et la géométrie. Parmi eux, la conjecture de Poincaré se distinguait par sa simplicité apparente et sa profonde challengingé.
Formulée en 1904 par Henri Poincaré, elle portait sur des sphères et la compréhension de l’univers. La conjecture affirmait : « Toute forme tridimensionnelle qui n’a pas de trous et est simplement connexe est, en essence, une sphère tridimensionnelle. »
Le Génie, la Solution et la Disparition
Grigori Perelman, mathématicien russe, a résolu la conjecture de Poincaré en 2003. Il a publié une série de trois articles détaillant sa démonstration, basée sur une technique appelée flux de Ricci. Sa solution a été confirmée en 2006. Même si beaucoup le considéraient comme une légende, il a refusé la médaille Fields et le million de dollars promis par le Clay Institute. Perelman vit désormais en reclus, refusant toute attention publique.
Questions Fréquentes (FAQ)
Q : Qu’est-ce que la conjecture de Poincaré ?
R : Elle stipule que toute forme tridimensionnelle sans trous et simplement connexe est, en essence, une sphère tridimensionnelle.
Q : qui a résolu la conjecture de Poincaré ?
R : Grigori Perelman.
Q : Qu’est-ce que les problèmes du millénaire ?
R : Sept problèmes mathématiques complexes pour lesquels le clay Mathematics Institute offrait une récompense d’un million de dollars par solution.
Q : Pourquoi Perelman a-t-il refusé les récompenses ?
R : Il ne souhaitait pas de célébrité ni de reconnaissance publique, préférant se concentrer sur son travail
Q : Qu’est-ce que le flux de Ricci ?
R : Une technique mathématique utilisée par Perelman pour « lisser » les formes complexes.
Résumé
| Élément | Détail |
| ———————— | ———————————————- |
| Problème Résolu | Conjecture de Poincaré |
| Mathématicien | Grigori perelman |
| Année de Résolution | 2003 |
| Récompenses Refusées | Médaille Fields, 1 million de dollars |
| Technique Utilisée | Flux de Ricci |
| Objectif du Problème | Compréhension de l’espace |






